Introdução à Recuperação de Informação #05 Modelo vetorial

👊😎 Saudações, galera! No último post da série de Introdução à Recuperação de Informação (RI) estudamos a proposta do modelo Booleano e fizemos uma implementação parcial usando o esquema de ponderação TF-IDF na linguagem Python. 👉 Hoje vamos estudar o modelo vetorial e fazer a implementação, novamente em Python.

🚀 Bora!

O modelo vetorial

O modelo vetorial, também conhecido pela sigla VSM (do inglês: vector space model) é um dos modelos mais usados para representar documentos textuais matematicamente em RI.

Nesse modelo, o documento é representado por um vetor de termos, em que cada um destes termos recebe um peso não binário representando sua a frequência no documento.

Da mesma forma, as consultas são representadas por vetores, o que possibilita fazer um cálculo de similaridade entre uma consulta q e um documento d_j. Isso significa que os termos da consulta são independentes, possibilitando casamentos parciais, melhorando o resultado da recuperação no contexto da relevância.

De acordo com Baeza-Yates e Ribeiro Neto (2013), o VSM é definido da seguinte maneira:

Para o modelo vetorial, o peso w_ij, associado ao par termo-documento (k_i, d_j) é não negativo e não binário. Os termos de indexação dão todos considerados mutuamente independentes e são representados por vetores unitários em um espaço com t dimensões, no qual t é o número de termos de indexação. As representações do documento d_j e da consulta q são vetores com t dimensões dadas por

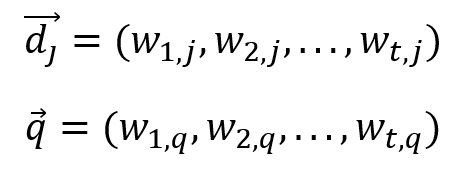
onde w_i,q é o peso associado ao par termo-consulta (k_{i, q}), com w_i,q ≥ 0.

O grau de similaridade entre o documento d_j e a consulta q, ou seja, sim(d_j, q) pode ser quantificado, por exemplo, pelo cosseno do ângulo entre esses dois vetores.

Esse valor é dado pelo produto interno dos vetores dj e q, dividido pela norma de d_j multiplicado pela norma de q, gerando um valor entre 0 e 1, obtido pela seguinte equação:

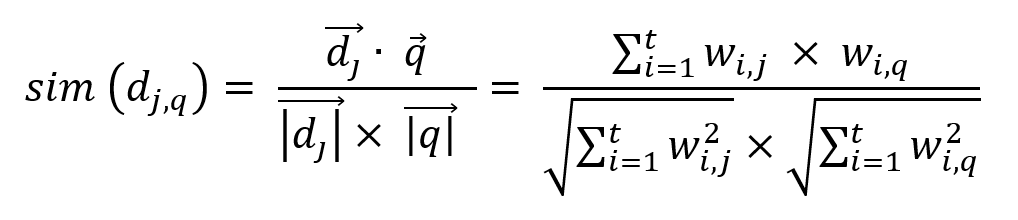
Representação de documentos

Para calcular a similaridade entre documentos e consultas, é necessário primeiro representá-los como vetores. O vetor do documento deve possuir t dimensões, onde t é o número de termos que compõem o documento. O valor de cada índice do vetor é o número de ocorrências de cada um dos termos t. Da mesma forma, a consulta q também deve possuir t dimensões, onde t é o número de termos presentes no documento. Entretanto, cada índice do vetor q possui um valor binário, ou seja, 0 ou 1. O valor é zero quando o termo não está presente no mesmo índice do vetor do documento, e o valor é 1 quando o termo está presente.

Assim, toma-se como exemplo os vetores: consulta q = [1,1], e o documento d_j = [1,3]. O primeiro termo (t₁) está presente uma vez em cada vetor. Por sua vez, o segundo termo (t₂) está presente 1 vez em q e 3 vezes em d_j. Ambos os vetores possuem a mesma quantidade de termos, logo, pode-se calcular a similaridade dentre eles. Na figura a seguir é possível observar a representação dos vetores num plano de coordenadas.

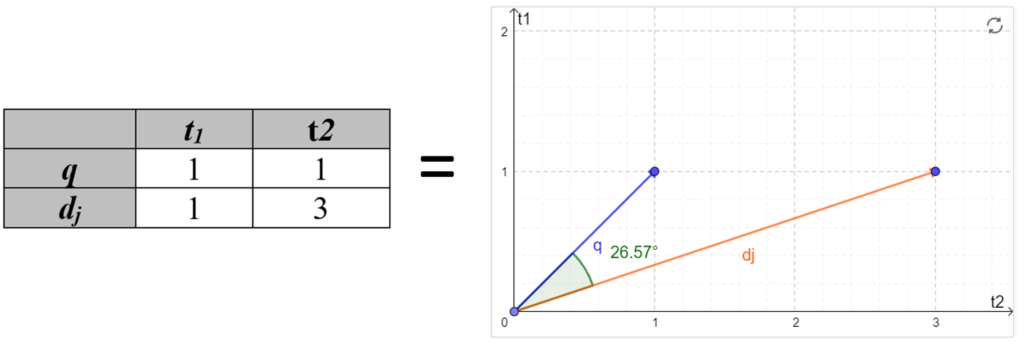
Se houvesse mais termos no documento d_j, seriam necessários outros eixos para representá-los no plano de coordenadas. Logo o gráfico teria que possuir t dimensões, pois t é sempre o número de termos do documento.

É importante destacar que a representação de vetores num plano de coordenadas possui duas características: a direção e a magnitude. A direção denota a relação do documento com os termos de indexação. Por sua vez, a magnitude denota o seu tamanho, ou seja, a quantidade de termos. Logo, quanto mais próximas estão as direções dos documentos, mais eles são similares. Se o ângulo entre q e d_j for igual a zero, mesmo com diferentes magnitudes, significa que os vetores apontam para a mesma direção, logo, são extremamente similares.

Calculando a similaridade entre documentos

No gráfico mostrado na Figura 2 há um ângulo de 26,57 graus entre os documentos, ou seja, consulta q e documento d_j. O cálculo do cosseno deste ângulo resulta no valor 0.8944271909999157, ou seja, arredondando com uma casa decimal, tem-se sim(d_j,q) = 0,9. 

Quanto mais próximo de 1, mais similares eles são. Quanto mais próximo de zero, menos similares.

Ranqueamento

No modelo vetorial o grau de similaridade é usado para a função de ranqueamento (ranking), classificando os resultados em ordem decrescente, do mais similar para o menos similar.

Por sua natureza relacionada à similaridade, o modelo vetorial permite que um documento seja recuperado mesmo que ele satisfaça parcialmente a consulta. Assim é possível determinar um limiar de similaridade, recuperando apenas os documentos com um grau mínimo aceitável.

Dependendo do tipo de aplicação, essa técnica pode ajudar a melhorar (ou “limpar”) os resultados, trazendo documentos mais relevantes e desprezando os menos relevantes.

Vantagens e Desvantagens

Segundo Baeza-Yates e Ribeiro Neto (2013), as vantagens do modelo vetorial são:

• O esquema de ponderação de termos melhora a qualidade da recuperação;
• Sua estratégia de casamento parcial permite a recuperação de documentos que aproximam as condições da consulta;
• A fórmula do cosseno ordena os documentos de acordo com seu grau de similaridade em relação à consulta;
• a normalização pelo tamanho do documento está naturalmente embutida no modelo.

Por sua vez, a desvantagem é que os termos de indexação são considerados independentes, desprezando-se principalmente sua semântica. Ou seja, o modelo vetorial, apesar de mais eficiente do que o modelo Booleano, ainda usa a abordagem bag of word (saco de palavra).

Mesmo assim, apesar de sua simplicidade e limitações o modelo vetorial é uma boa estratégia, considerando sua simplicidade e bons resultados em coleções genéricas de documentos textuais.

Implementação em Python 3

🤙 Hands on! Vamos usar a liguagem Python para implementar o modelo vetorial, usando a fórmula do cosseno para fazer o ranqueamento dos resultados.

Se você não possui familiaridade com a linguagem Python, você pode se apoiar na lógica apresentada aqui e implementar em outra linguagem.

É importante destacar que essa implementação é simples, ou seja, foi realizada em somente um arquivo .py, ignorando conceitos de código limpo, programação orientada a objetos, etc.

Importando as bibliotecas necessárias

Para esta implementação, vamos usar basicamente os pacotes NLTK (Natural Language Toolkit) e Numpy. O primeiro possui uma série de classes para lidar com processamento de linguagem natural. Já o segundo é uma biblioteca usada para ciência de dados e manipulações matemáticas.

Assim, vamos importar as seguintes bibliotecas:

• NLTK
  • word_tokenize: transforma textos em arrays – um documento se torna um array de termos ou palavras;
  • stopwords: define o conjunto de stopwors que serão usadas no preprocessamento;
  • WordNetLemmatizer: usada para fazer a lematização das palavras, ou seja, reduzir as palavras à sua forma original, no singular e no masculino;
• Numpy
  • numpy: para calcular o produto interno dos vetores;
  • numpy.linalg: para calcular as normas dos vetores;
• math: usado para operações matemáticas genéricas.

Assim, os imports fica da seguinte maneira:

#the nltk has classes to deal with natural language
import math
from nltk.tokenize import word_tokenize
from nltk.corpus import stopwords
from nltk.stem import WordNetLemmatizer

#the numpy package has too many classes do deal with data and math
import numpy as np
from numpy.linalg import norm

Criando o dataset e fazendo o pré-processamento

Agora vamos criar um simples dataset, e fazer o seu pré-processamento, como fizemos no post anterior. Note que após o resultado do pré-processamento, a variável do tipo list cleanDataset irá conter o dataset “limpo”.

#the dataset or collection
dataset = [
    "Earth orbits Sun, and the Moon orbits Earth. The Moon is a natural satellite that reflects the Sun's light.",
    "The Sun is the biggest celestial body in our solar system. The Sun is a star. The Sun is beautiful.",
    "Earth is the third planet in our solar system.",
    "The Sun orbits the Milky Way galaxy!"
]

#a variable to store the stopwords
stopWords = stopwords.words('english')
#the lemmatizer 
lemmatizer = WordNetLemmatizer()
#an array to store the clean dataset, after the preprocessing
cleanDataset = []

#store the clean dataset
cleanDataset = []

#perform the precprocessing
#for each doc present in dataset, do...
for doc in dataset:
    #tokenize (a doc is an array of words) the doc and convert to lower case
    tokenDoc = word_tokenize(doc.lower())
    #a variable to store a clean doc
    cleanDoc = []
    #for each word in tokenDoc, do...
    for word in tokenDoc:
        #if the word is alphanumeric and is not present in stopwords, then...
        if(word.isalnum() and word not in stopWords):
            #extracts the lemma and add it to cleanDoc array
            cleanWord = lemmatizer.lemmatize(word)
            cleanDoc.append(cleanWord)
    #add the processed doc to cleanDataset array
    cleanDataset.append(cleanDoc)

#show clean Dataset
print(cleanDataset)

Criando a função para calcular a similaridade

Agora vamos criar a função para calcular a similaridade usando a biblioteca Numpy. Note que é possível que o resultado da equação da similaridade retorne um tipo NAN (not a number), significando que não há nada de similar entre os documentos. Logo, precisamos tratar isso e retornar zero. Veja como fica a função:

#define a function to calculate the cosine similarity
#we are using the numpy methods
def cosineSimilarity(query, doc):
    sim = np.dot(query,doc)/(norm(query)*norm(doc))
    if(math.isnan(sim)):
        return 0
    else:
        return sim

Criando o script para realizar a recuperação de informação

Antes de criar o script de recuperação, vamos definir três variáveis: a) uma para armazenar os resultados da query; b) uma para armazenar a própria query; c) uma para atribuir um id em cada documento. Veja:

#an array to store the results of query
results = []
#define the query
query = ['sun', 'star']
#a variable to define the id of document in the results
id = 1

Agora vamos criar o script que itera sobre o dataset, calcula a similaridade entre um documento e a query dada, e adiciona o resultado em uma variável do tipo list que é ordenado de maneira decrescente.

#the script to calculate the similary for all docs
#for each doc in cleanDataset, do...
for doc in cleanDataset:
    #create the vocabulary of doc
    vocabulary = list(set(doc))

    #create two arrays with zeros to represents the query and the doc
    #vectors must have the same size to calculate similarity
    vecDoc = [0] * len(vocabulary)
    vecQuery = [0] * len(vocabulary)

    #for each word in doc, do...
    for word in doc:
        #fill the vecDoc with a weight number considering the term frequency of the word
        vecDoc[vocabulary.index(word)] +=1

    #do the same with query, but, when the term of query is not present in doc, the term frequency is zero. 
    for word in query:
        if word in vocabulary:
            vecQuery[vocabulary.index(word)] += 1

    #calculate the cosine similariy
    cosine = cosineSimilarity(vecDoc, vecQuery)
    #add the result in results list
    results.append({"id":id, "score" : round(cosine, 5)})
    #increment the id
    id+=1
#show the results
print(results)

Ordenando os resultados

Agora que temos na variável do tipo results os resultados da query, é necessário ordenar do mais similar para o menos similar. Para isso, vamos usar a função sort. Veja:

#a function to sort the results by score
def mySort(obj):
    return obj['score']

#sort the result in descending way by similarity score
results.sort(key=mySort, reverse=True)

#show the results
for result in results:
    print(result)

Conclusão

Neste post vimos com mais detalhes o modelo vetorial (VSM) e como implementá-lo na linguagem Python.

Como já citado, o VSM é um modelo que apresenta resultados satisfatórios para coleções genéricas de documentos.

No próximo post iremos discutir o modelo probabilístico. Até lá! 👊😎

Referências

O código apresentado está disponível no repositório do GitHub: https://github.com/jlgregorio81/ir_vector_model

BAEZA-YATES, R.; RIBEIRO-NETO, B. Recuperação de Informação: Conceitos e Tecnologia das Máquinas de busca. 2 ed. Porto Alegre: Grupo A, 2013.