Introdução à Recuperação de Informação #04 Modelo Booleano

👊😎 Saudações, galera! No post anterior vimos como representar documentos textuais logicamente. Isso é um conceito fundamental em Recuperação da Informação (RI)
👉 Neste post vamos implementar parcialmente o modelo Booleano na linguagem Python. Digo parcialmente, pois iremos implementar um exemplo simples, apenas para entender a proposta do modelo, visto que ele possui uma série de limitações.
👍 Se você não conhece a linguagem Python, mas conhece outra, isto é, domina os fundamentos da lógica de programação e estruturas de dados, você poderá implementar esse modelo em outra linguagem.
🚀 Bora!
O modelo Booleano
Como vimos anteriormente, o modelo Booleano considera que os termos de indexação da consulta podem estar presentes ou ausentes no documento (pesos binários). Assim uma consulta q é composta por termos de indexação ligados pelos operadores booleanos not, and e or. Por sua simplicidade, foi o modelo mais usados no passado por muitos sistemas bibliográficos.
Segundo Baeza-Yates e Ribeiro Neto (2013), o modelo Booleano é definido da seguinte maneira:
No modelo Booleano, uma consulta q é uma expressão Booleana convencional sobre termos de indexação. Considere c(q) como qualquer um dos componentes conjuntivos da consulta. Dado um documento dj, sendo c(dj) seu componente conjuntivo de documento correspondente, então a similaridade entre o o documento e a consulta é definida por
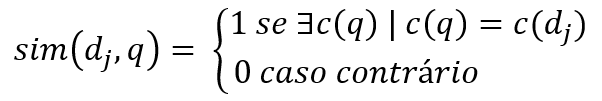
Se sim(dj, q) = 1, então o modelo Booleano provê que o documento dj seja relevante à consulta q (e ele pode não ser). Caso contrário, a predição é que o documento não seja relevante.
A principal vantagem desse modelo é sua simplicidade, considerando pesos binários para os termos de indexação.
Sua principal desvantagem é o fato de não existir uma função de ranqueamento, o que leva à recuperação de muitos ou poucos documentos, dependendo de como a consulta é formulada. Ademais, a criação de consultas booleanas não é adequada à maioria dos usuários.
De fato, a simples existência de um termo da consulta em um documento não pode ser usado como fator de relevância. Assim, é necessário implementar a ponderação dos termos de indexação, que permite a utilização de pesos não binários, melhorando a qualidade da recuperação e permitindo a formulação de um sistema de ranqueamento.
Ponderação TF-IDF
A frequência do termo no documento (TF – Term Frequency) e a frequência inversa do termo (IDF – Inverse Document Frequency), ou seja, o quanto importante ele é na coleção, compõem o esquema de ponderação TF-IDF, o mais popular em RI.
O valor (ou score) TF-IDF de um termo de indexação aumenta proporcionalmente ao número de ocorrências dele num documento. Entretanto, esse valor é ajustado pela frequência do referido termo na coleção (ou corpus). Isso ajuda a evitar discrepâncias, como por exemplo no caso de uma palavra ser relevante no documento, mas irrelevante na coleção.
É importante salientar que quanto mais frequente é uma palavra, menos importante ela é pra discriminar um documento. Por outro lado, quanto mais rara, mais discriminativa ela é.
O esquema de ponderação TF-IDF é dado por:
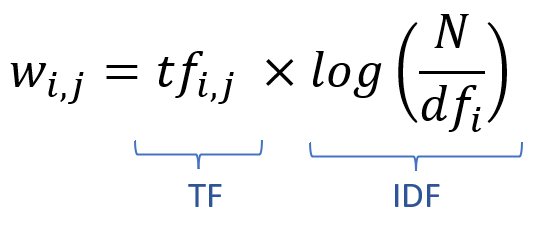
- wi,j : peso de um termo i no documento j;
- tfij: a frequência do termo i no documento j;
- N: o número de documentos da coleção
- dfi: número de documentos que contém o termo i.
Exemplo
Considere a seguinte coleção de documentos d1, d2, d3 e d4:
- Earth orbits Sun, and the Moon orbits Earth. The Moon is a natural satellite that reflects the Sun’s light.
- The Sun is the biggest celestial body in our solar system. The Sun is a star. The Sun is beautiful.
- Earth is the third planet in our solar system.
- The Sun orbits the Milky Way galaxy!
Considere também a consulta q = “Sun”. Assim, aplicando a equação TF-IDF mostarda na figura anterior, temos a matriz:
| q = “Sun” | TF | IDF | TF-IDF |
| d1 | 2 | log(4/3) = 0,12494 | 0,24988 |
| d2 | 3 | log(4/3) = 0,12494 | 0,37482 |
| d3 | 0 | log(4/3) = 0,12494 | 0 |
| d4 | 1 | log(4/3) = 0,12494 | 0,12494 |
Uma vez que temos os pesos TF-IDF para um termo, é possível fazer o ranqueamento. Nesse caso, o ranking seria ordenado assim: d2, d1, d4. O documento d3, como possui score zerado, poderia não aparecer, ou aparecer no final, como um documento irrelevante à consulta q.
Nesse momento você deve estar ser perguntando: “Ora, o documento d3, apesar de não falar diretamente sobre o Sol, cita o sistema solar, que é um assunto relacionado, então, ele também seria relevante”.
Claro que sim! Entretanto, estamos usando a abordagem bag of word (saco de palavras), que considera apenas o aspecto sintático dos termos e não sua semântica. Tenha isso em mente!
Implementação em Python 3
🤙 Hands on! Vamos implementar o modelo Booleano parcialmente na linguagem Python, usando o TF-IDF para fazer o ranqueamento dos resultados.
Se você não possui familiaridade com a linguagem Python, você pode se apoiar na lógica apresentada aqui e implementar na sua linguagem favorita.
É importante destacar que essa implementação é simples, ou seja, foi realizada em somente um arquivo .py, ignorando conceitos de código limpo, programação orientada a objetos, etc.
Importando as bibliotecas necessárias
Uma das bibliotecas mais usadas para trabalhar com análise de textos e, consequentemente, com RI na linguagem Python, é a biblioteca NLTK – Natural Language Toolkit. Também vamos usar a biblioteca math, que disponibiliza funções para cálculos matemáticos.
Assim, vamos usar as seguintes funções e classes:
- word_tokenize: transforma textos em arrays – um documento se torna um array de termos ou palavras;
- stopwords: define o conjunto de stopwors que serão usadas no preprocessamento;
- WordNetLemmatizer: usada para fazer a lematização das palavras, ou seja, reduzir as palavras à sua forma original, no singular e no masculino;
- math: vamos usar a função log para calcular o IDF.
Codificando
from nltk.tokenize import word_tokenize
from nltk.corpus import stopwords
from nltk.stem import WordNetLemmatizer
from math import logUma vez que as importações foram realizadas, vamos criar o seguinte dataset:
#the dataset or collection
dataset = [
"Earth orbits Sun, and the Moon orbits Earth. The Moon is a natural satellite that reflects the Sun's light.",
"The Sun is the biggest celestial body in our solar system. The Sun is a star. The Sun is beautiful.",
"Earth is the third planet in our solar system.",
"The Sun orbits the Milky Way galaxy!"
]Agora vamos criar três variáveis para armazenar as stopwords, instanciar o lematizador e criar um array para armazenar o dataset “limpo”, após o pre-processamento.
#a variable to store the stopwords
stopWords = stopwords.words('english')
#the lemmatizer
lemmatizer = WordNetLemmatizer()
#an array to store the clean dataset, after the preprocessing
cleanDataset = []O próximo passo é realizar o pré-processamento. Para isso vamos definir o seguinte script:
#perform the precprocessing
#for each doc present in dataset, do...
for doc in dataset:
#tokenize (a doc is an array of words) the doc and convert to lower case
tokenDoc = word_tokenize(doc.lower())
#a variable to store a clean doc
cleanDoc = []
#for each word in tokenDoc, do...
for word in tokenDoc:
#if the word is alphanumeric and is not present in stopwords, then...
if(word.isalnum() and word not in stopWords):
#extracts the lemma and add it to cleanDoc array
cleanWord = lemmatizer.lemmatize(word)
cleanDoc.append(cleanWord)
#add the processed doc to cleanDataset array
cleanDataset.append(cleanDoc)
#print the cleanDataset
print(cleanDataset)Agora vamos criar duas funções, uma para calcular o TF e outra pra calcular o IDF.
#a function to calculate term frequency
def termFrequency(term, doc):
count = 0
#for each word in doc, do...
for word in doc:
#if the term is the same as the word, then increment count
if term == word:
count += 1
return count
#a function to calculate the inverse term frequency
def inverseTermFrequency(term, dataset):
freq = 0
#get the number of elements
size = len(dataset)
#for each doc in dataset, do...
for doc in dataset:
#if term is present in doc, increment the frequency...
if term in doc:
freq += 1
#return the result - using log at base 10
return log(size/freq, 10)Agora vamos criar uma outra função que usa essas funções pra gerar os scores TF-IDF.
#a function to generate the TF-IDF scores
def tfidfScores(term, dataset):
#calculate the inverse term frequency
idf = inverseTermFrequency(term, dataset)
#an array to store the scores
scores = []
#a variable to create the id of the document
id = 1
#for each doc in dataset, do...
for doc in dataset:
#calculate the tfidf for doc
tfidf = termFrequency(term, doc) * idf
#add the score in scores array - round with five decimals
scores.append({"id" : id, "score" : round(tfidf,5)})
#increment the id
id += 1
return scoresFinalmente, vamos gerar os scores TF-IDF e mostrá-los de maneira simples, usando a função print.
#generate the tfidf scores
tfidf = tfidfScores("sun", cleanDataset)
#create a function to define the key to sort
def mySort(obj):
return obj['score']
#sort the scores
tfidf.sort(key=mySort, reverse=True)
#print the result
print(tfidf)Conclusão
Apesar dessa implementação parcial e simples, acredito que os conceitos básicos do modelo Booleano, principalmente do esquema de ponderação TF-IDF ficaram claros.
As limitações do modelo Booleano fizeram com que surgissem modelos mais eficientes, que exploraremos nas próximas postagens.
👊😎 Até lá!
Referências
👉 O repositório do GitHub com o código implementado está disponível aqui: https://github.com/jlgregorio81/ir_boolean_model_tfidf
BAEZA-YATES, R.; RIBEIRO-NETO, B. Recuperação de Informação: Conceitos e Tecnologia das Máquinas de busca. 2 ed. Porto Alegre: Grupo A, 2013.



